Another "real work" project that I can share (that's kind of the point): a family of open-weights LLMs. Rewriting thousand-line layers (for training) in 3 lines (for the reference implementation) was fun.
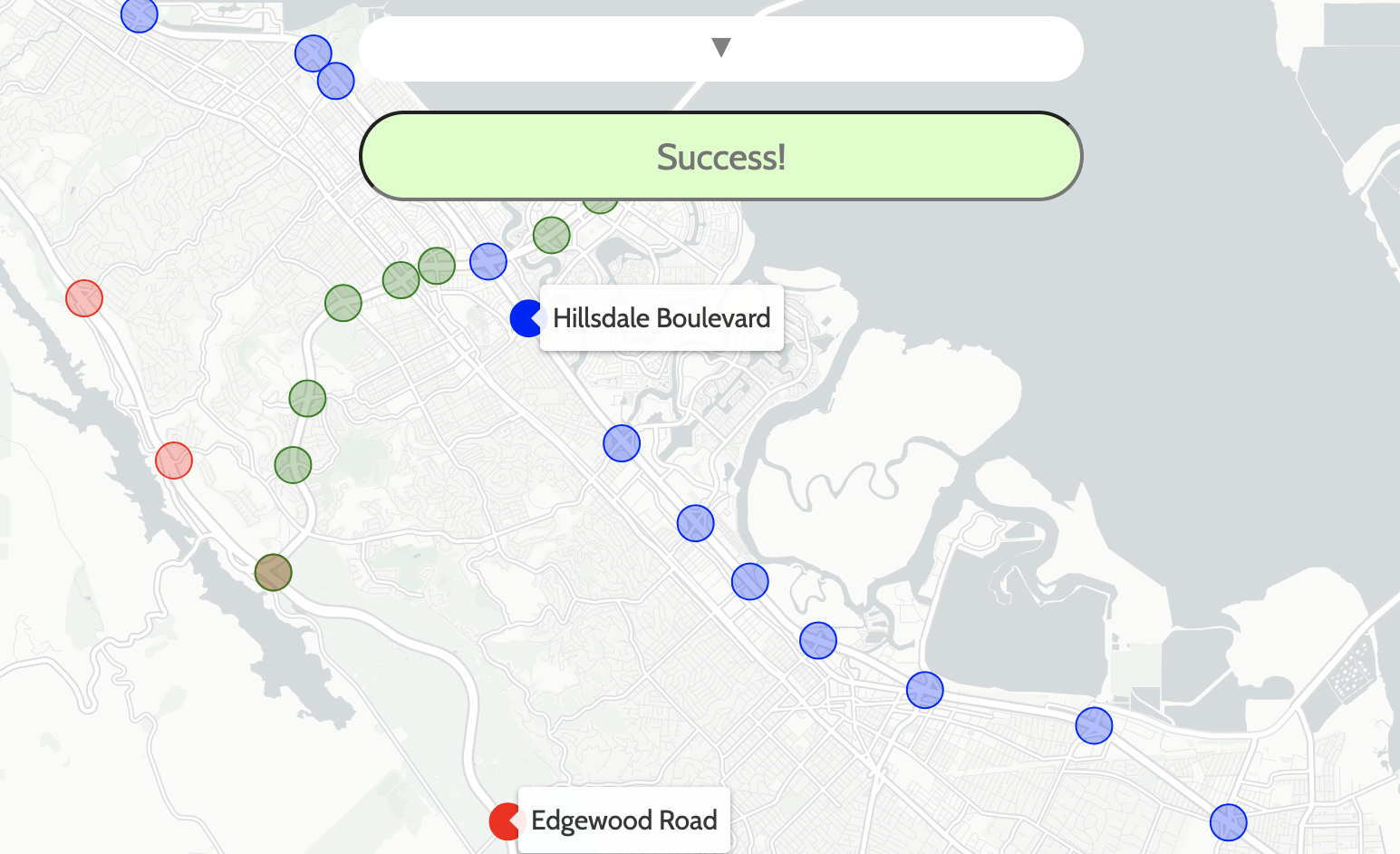
Following the viral London Metro Memory game, I pondered what the equivalent would be for the Bay Area. This is the result.
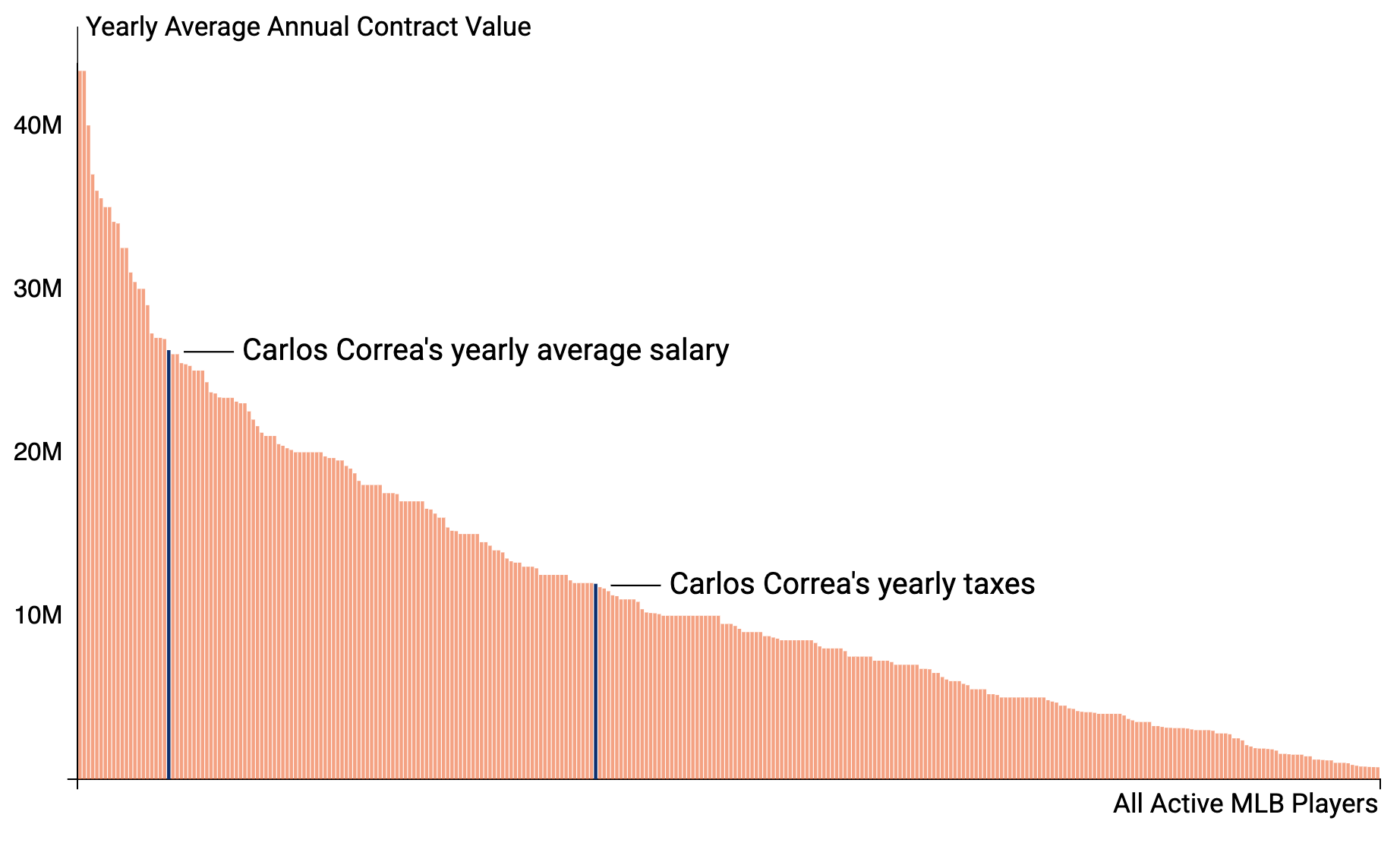
A quick vacation project digging into some fun facts that surfaced after the Mets offered a lot of money to Carlos Correa (and others).

My first (and so far, only) public-facing project at DeepMind. Dramatron is a script writing tool that leverages large language models. You can read about Dramatron here.

A personal coding and cartography project. I created an algorithm for filling arbitrary polygons with hexagons, ran the algorithm on different geographic geometries, and added some visual flair to the results. More here.
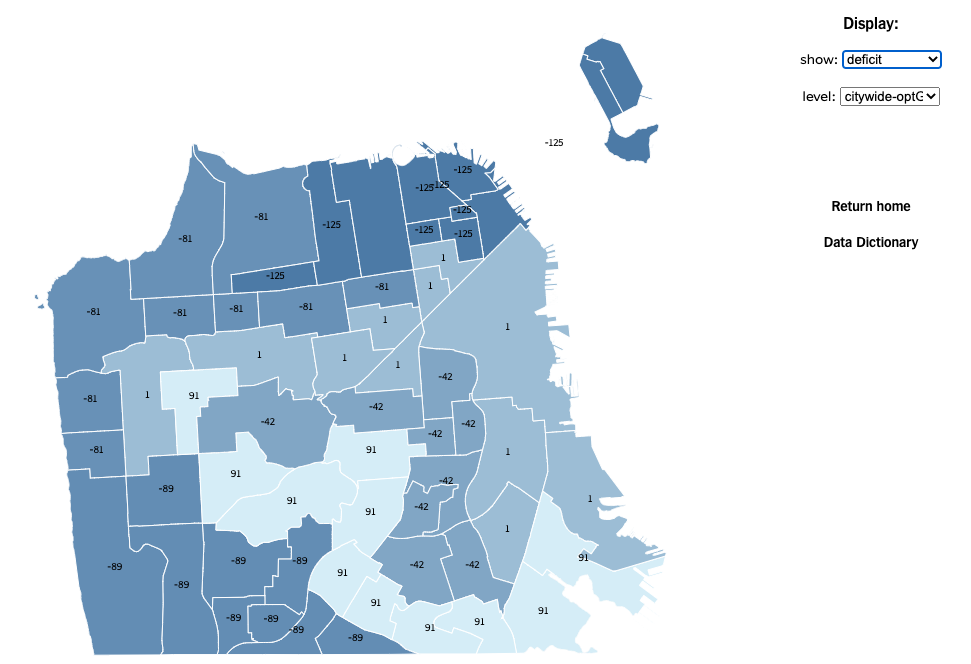
I worked with a team at Stanford on redesigning the seat assignment algorithm for the San Francisco Unified School District. Read our paper here.
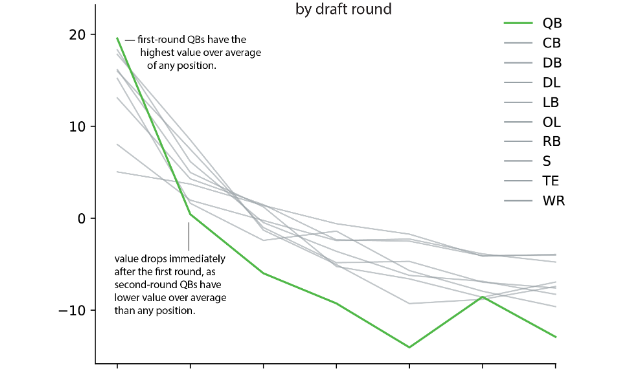
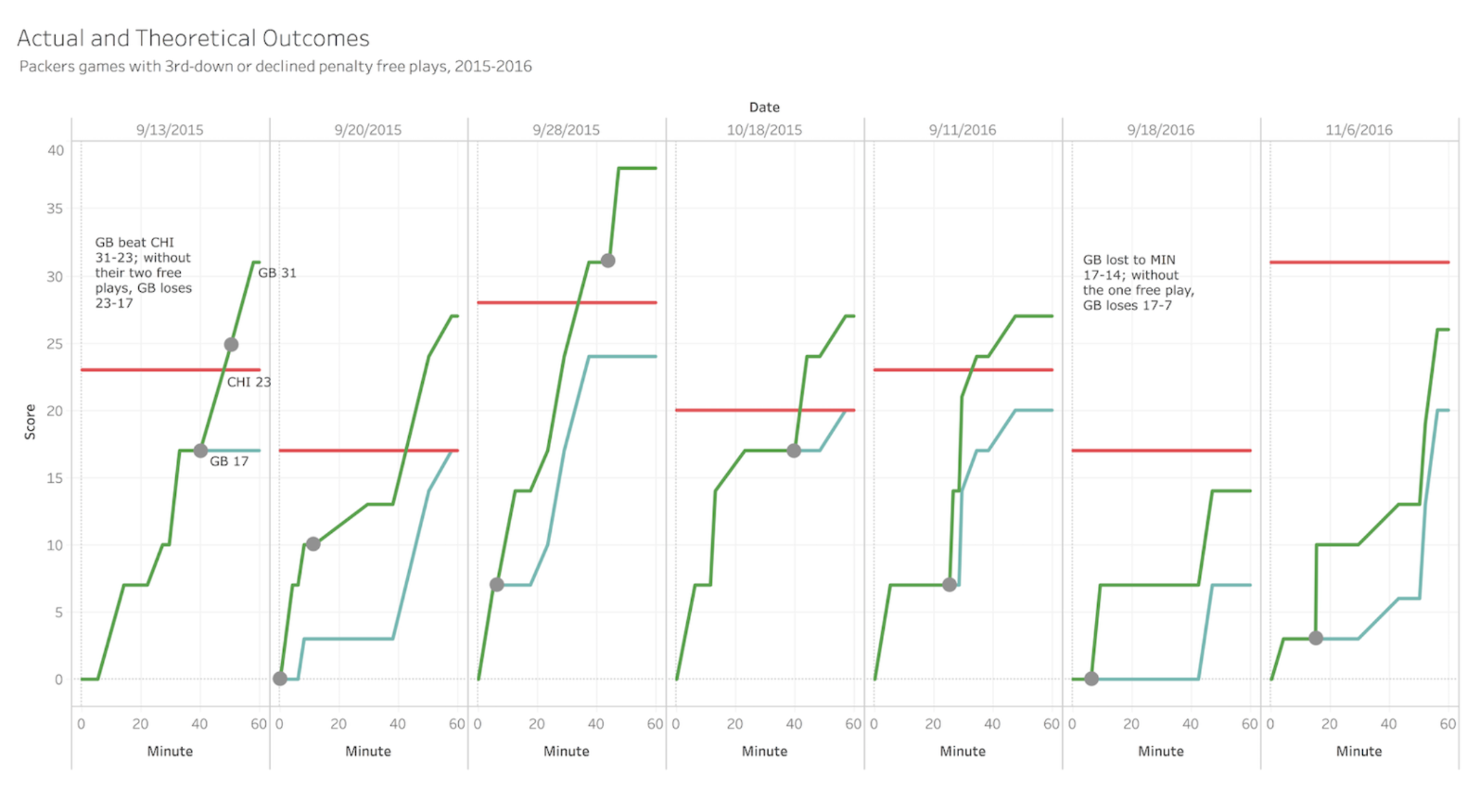
Out of curiosity, I examined the value of different picks and positions in the NFL draft, each team's historical draft success, and which conferences have provided the most valuable picks over time. Read the report.

For a Stanford seminar on the aristic legacy of World War II, I wrote about how modern attitudes towards American involvement obscure historical reality and leave us vulnerable to the reemergence of evil. Read the full piece.
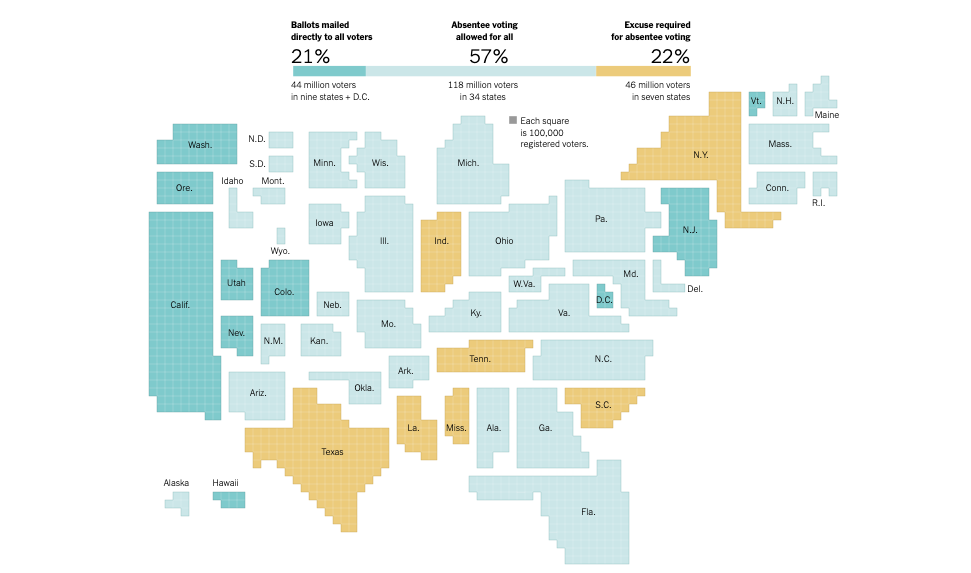
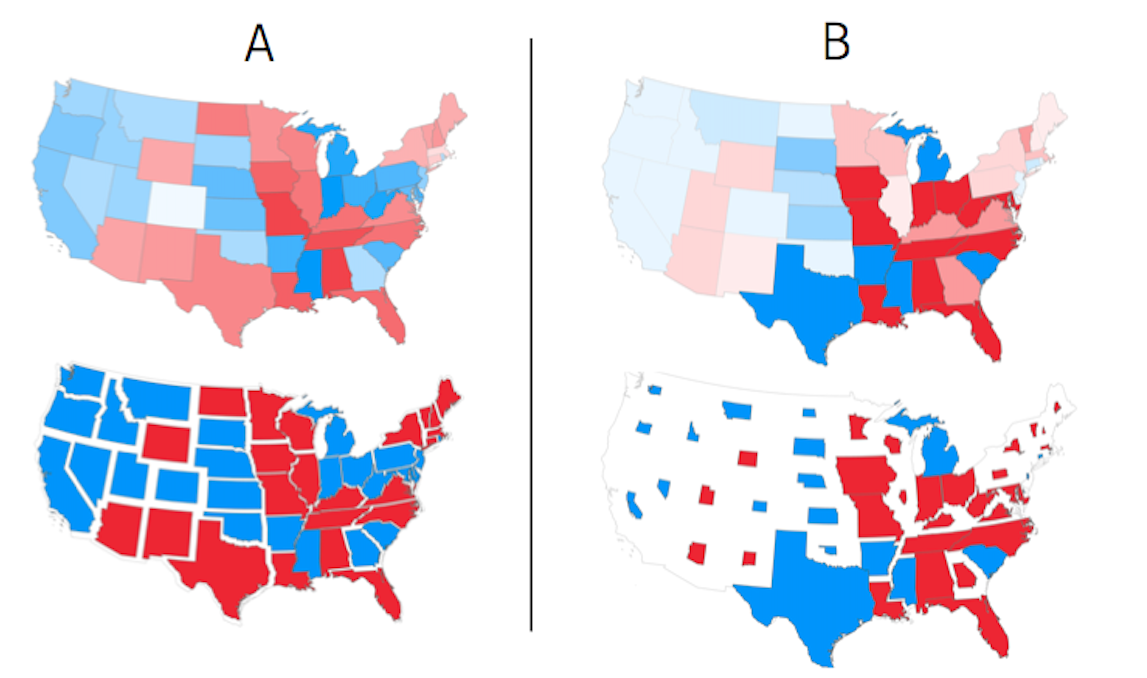
More people were eligible to vote by mail in 2020 than ever before. While at the New York Times, I conducted an investigation on each state's vote-by-mail rules. Read the article.
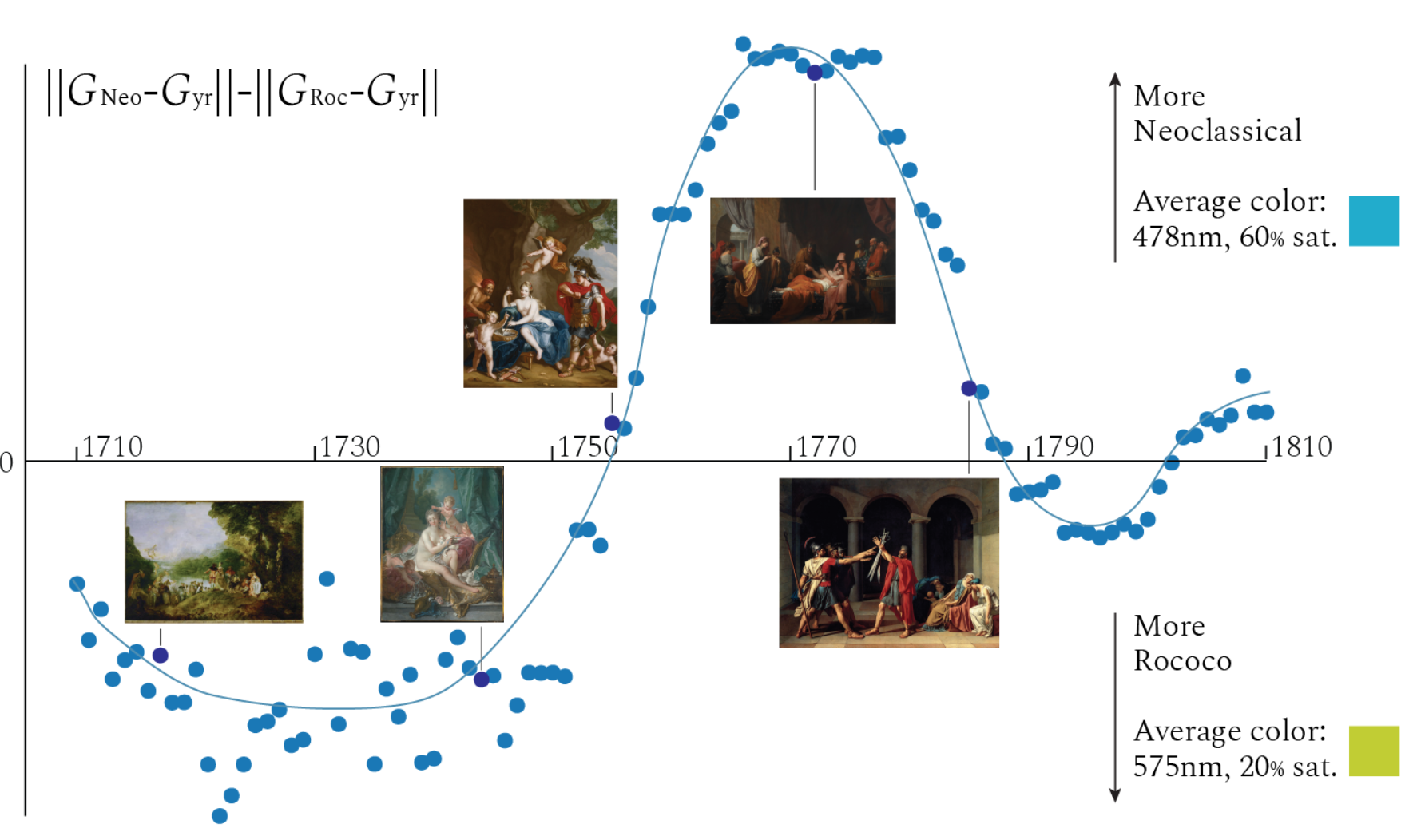
I analyzed the transition from Rococo to Neoclassical color palettes during the 18th century by fitting Gaussian curves to chromatic coordinates. Read the full paper here.
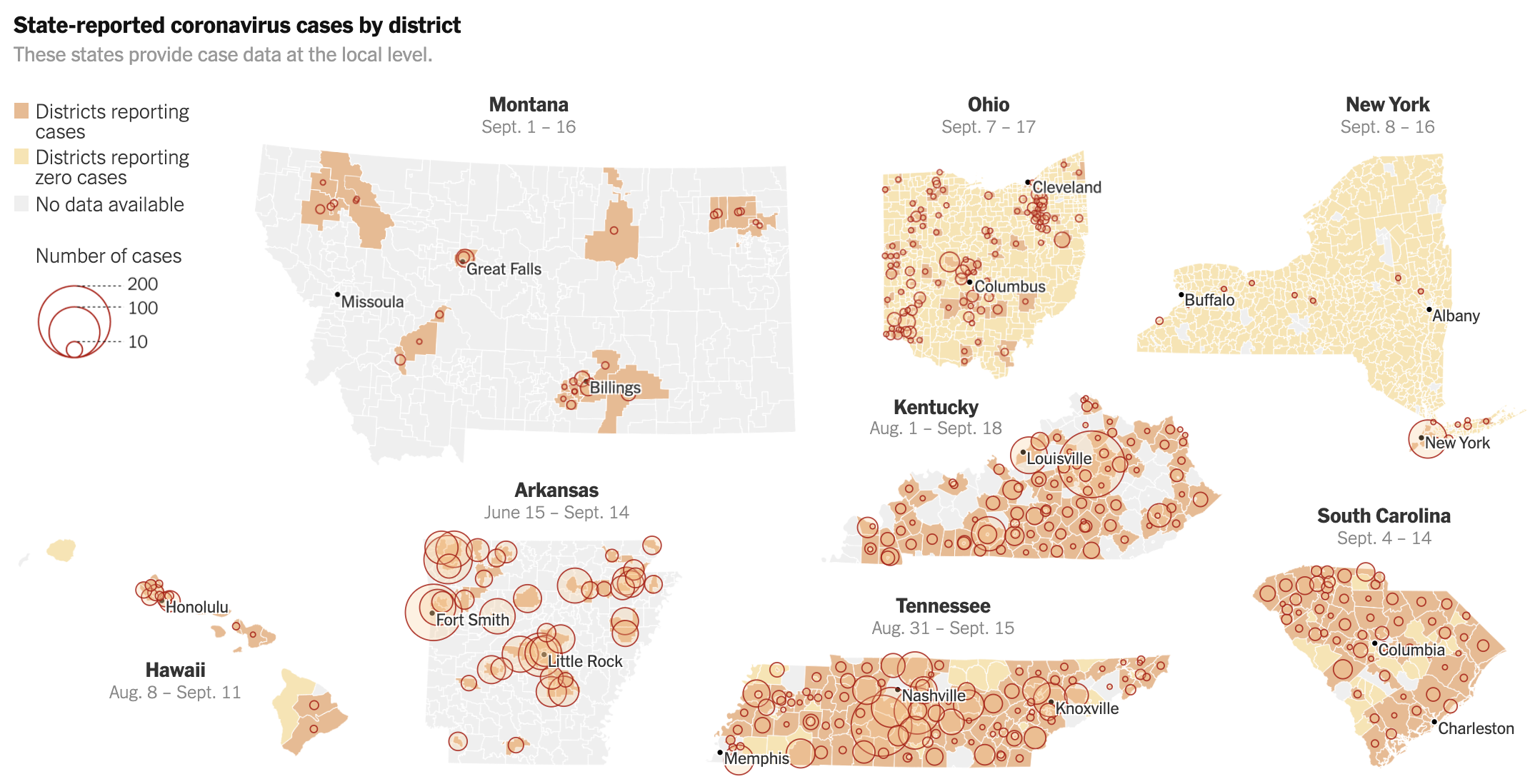
I spent much of lockdown in 2020 covering Covid-19 and its impacts on the nation. I wrote about cases in Latino communities, K-12 schools, and contributed to this piece memorializing the first 100,000 American lives lost.
I worked with Prof. Kären Wigen and Dr. Martin Lewis on Seduced by the Map, a multimedia, online, open-access work critiquing the idea of the ubiquitous "nation-state." Access the in-progress work here.
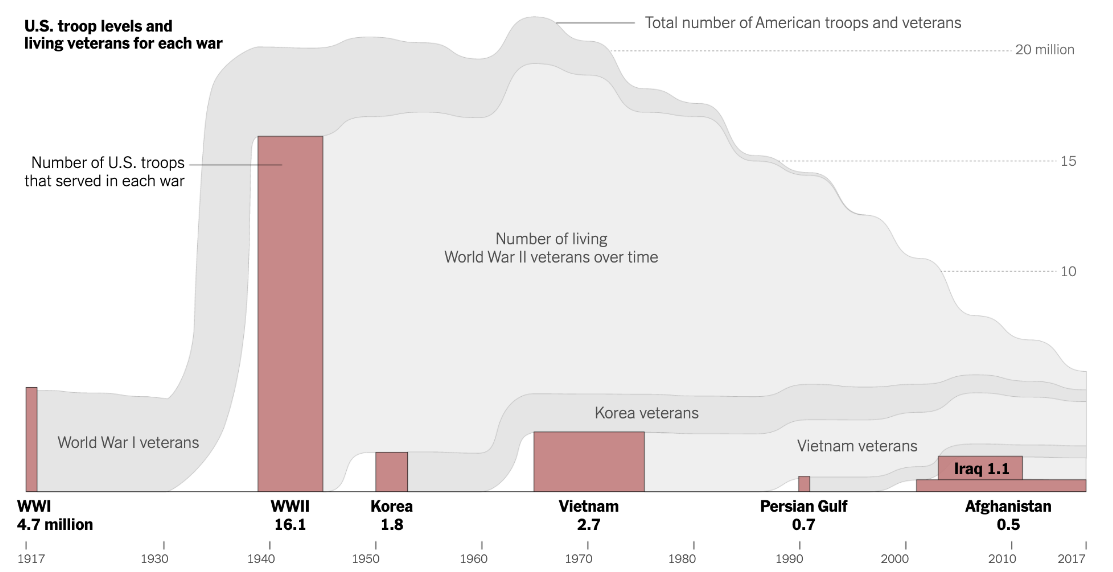
As the war in Afghanistan came to a close, I wrote a piece for the New York Times assessing its cost—human and monetary—and hypothesized why it garnered less national attention than previous conflicts. Full story here.
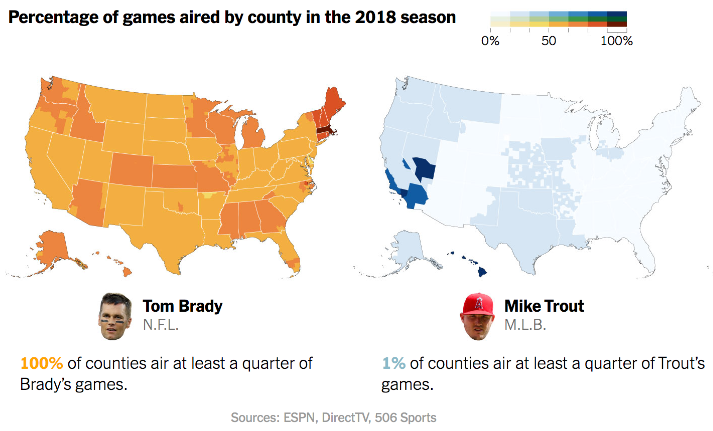
While at the Times, I was fortunate enough to pitch, research, and write a piece explaining the popularity of baseball and some common misconceptions about the sport's decline. Read the piece here.
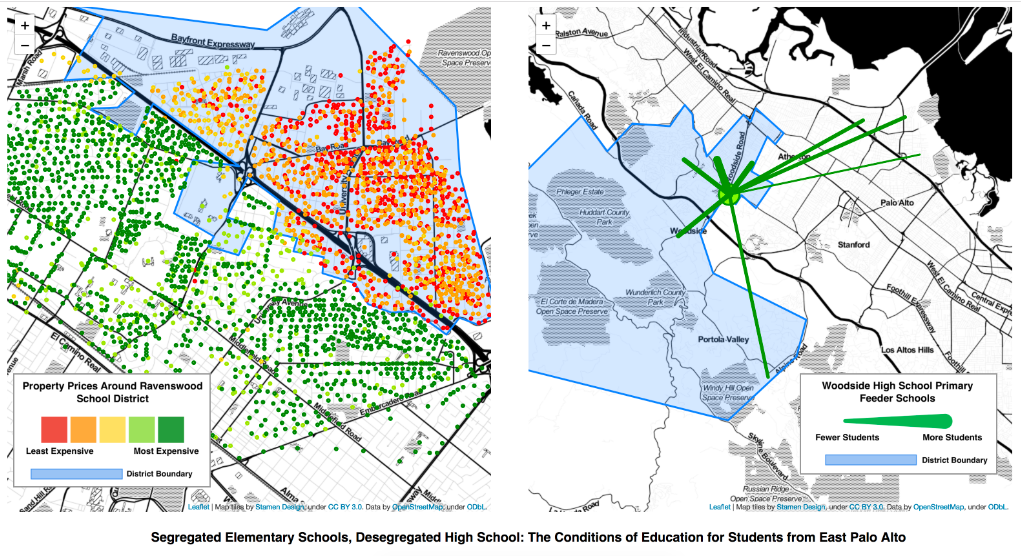
Through a couple of Stanford courses, I researched the educational inequities in the Bay Area, and assesesed the impact of school segregation and desegregation policies. Check out this interactive graphic or read the report.